Немного теории обнаружения аномалий
Рассмотрим оператор присваивания
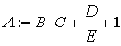 |
1 |
Для семантически корректного вычислительного процесса в контексте данного оператора должны выполнятся следующие соотношения между абстрактными размерностями параметров (A, B, C, D, E, CONST_1):
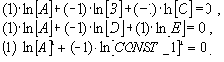 |
2 |
Эти соотношения, так называемые инварианты подобия, позволяют однозначно определить эталон "правильного" функционирования некоторой распределенной вычислительной системы. При этом вычислительный процесс семантически корректен, если соответствующая система уравнений размерностей имеет среди множества векторов-решений хотя бы один, состоящий из всех ненулевых компонент. Действительно, предположим, что, это не так, и среди параметров вычислительного процесса определенной размерности появился параметр тождественно равный нулю при любых значениях других параметров. Это указывает на безразмерность нового параметра. Однако это невозможно, так как противоречит исходному условию определения размерностей параметров вычислительного процесса.
В результате становится возможным предложить универсальную методику обнаружения аномалий на основе инвариантов подобия. Основная идея этой методики заключается в распознавании аномалий вычислительных процессов с помощью сравнения значений инвариантов подобия реальных вычислительных процессов с эталонными значениями инвариантов. К достоинствам методики относится то, что удалось явно исключить шаг выделения независимых параметров вычислительного процесса на основе эвристических алгоритмов. Использование достаточно строгого требования отличия компонент вектора решения от нуля позволило разработать полностью автоматический детерминированный алгоритм обнаружения аномалий. В частности, для вывода инвариантов подобия семантически корректного вычислительного процесса необходимо построить матрицу R-вида:
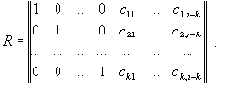 |
3 |
или
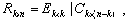 |
4 |
где E - единичная матрица, k и n - количество строк и столбцов исходной матрицы коэффициентов размерностей S соответственно.
Для построения матрицы R достаточно воспользоваться следующими операциями:
Метод построения матрицы R аналогичен методу Жордана-Гаусса, но при этом обладает следующими особенностями. Во-первых, осуществляется двойной обход алгоритма: сначала в прямом (сверху вниз), а затем в обратном (снизу вверх) направлении. Во-вторых, перестановка столбцов производится в тех случаях, когда ненулевое значение ячейки в пределах первых k столбцов (являющееся не первым ненулевым по счету в строке) невозможно привести к нулю из-за отсутствия в данном столбце иных ненулевых членов.
Заметим, что матрица R идентична матрице S за исключением возможных перестановок столбцов, то есть справедливо выражение
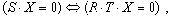 |
5 |
Таким образом, выражение (5) позволяет использовать матрицу R вместо матрицы S для вывода инвариантов подобия семантически корректных вычислительных процессов в распределенных вычислительных системах на основе TCP/IP. Для наличия среди первых k значений вектора-решения системы ограничений размерности i-й компоненты, тождественно равной нулю, необходимо и достаточно, чтобы в i-й строке матрицы C в формуле (4) все элементы были равны нулю. Действительно, пусть в i-й строке матрицы C существует хотя бы один ненулевой элемент (например, в позиции j ). Тогда, установив равными нулю все (n-k) последних переменных за исключением (k+j)-й, получим следующее равенство:
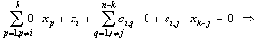 |
6 |
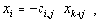 |
7 |
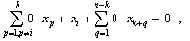 |
8 |
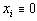 |
9 |
Переменные, соответствующие остальным столбцам матрицы R, - зависимые. Таким образом, предлагаемая методика (с полным построением матрицы R) представляет собой единую, универсальную методику обнаружения аномалий вычислительных процессов в распределенных вычислительных системах на основе TCP/IP. Отметим некоторые особенности предлагаемой методики. На практике возможна некоторая модификация методики, в частности, вариация алгоритма построения матрицы R. Например, выделение базисных переменных и необходимые вычислительные преобразования над R производятся при добавлении к ней каждой новой строки. Цель модификации - формирование на каждом шаге анализа матрицы ограничений размерности, приведенной к виду (3).
Данный алгоритм позволяет:
полностью исключить вычислительные расходы, связанные с поздней (согласно алгоритму Жордана-Гаусса) перестановкой столбцов матрицы;
уменьшить количество вычислительных операций в ходе выделения единичной матрицы в левой части матрицы R.
Алгоритм требует дополнительного хранения перестановочной матрицы T на всем этапе контроля семантической корректности вычислительного процесса, что несколько замедляет доступ к элементам матрицы. Однако использование эффективных структур данных позволяет свести дополнительные расходы к минимуму.
Отметим, построение матрицы R в ходе контроля семантической корректности вычислительного процесса позволяет обнаружить семантическую ошибку до окончания всего построения (однако вовсе не обязательно, что критерий корректности нарушится именно в момент добавления информации об ошибочной строке процесса). Данный факт является определенным достоинством предлагаемой инженерной методики обнаружения аномалий в случае наличия в сети передачи данных большого количества ошибочных пакетов (умышленно либо неумышленно порожденных). В этом случае станция-получатель L, еще не декодировав сообщение полностью, может принять решение об его игнорировании. Данную особенность можно использовать при создании комплексной системы защиты от атак класса "отказ в обслуживании".
При этом в нормальных условиях функционирования досрочные отклонения пакетов не влияют на среднестатистическую вычислительную трудоемкость. В связи с тем, что доля аномальных реализаций процессов стека сетевых протоколов стремится к нулю.
Другая особенность рассмотренной методики - наличие нескольких независимых между собой групп размерностей переменных. Примером могут служить счетчики, обрабатываемые данные, сетевые адреса, параметры протоколов. В результате, почти для всех сетевых протоколов множество параметров можно разбить на подмножества общим числом от 2 до 5-10, в зависимости от специфики протокола. Аналогами данных подмножеств в пространстве образов отображения ? являются связные компоненты графа. Внутри каждого подмножества аналогично основному множеству можно выделить базисные и зависимые переменные. Отмеченная особенность позволяет с минимальными вычислительными затратами привести матрицу S путем перестановки строк и столбцов к блочно-диагональному виду:
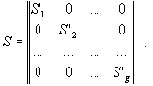 |
10 |
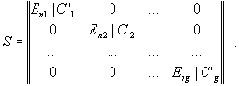 |
11 |
