Оценка быстродействия предлагаемой методики
Рассмотрим систему размерностей в терминах теории графов. В этом случае процесс проверки существования нетривиального или не имеющего нулей решения системы линейных уравнений сводится к проверкам подсистем, имеющих ранг, равный количеству содержащихся в них переменных. В фактор-множестве (G/?)/?' подсистемам, обладающим подобными свойствами, соответствуют простые циклы (везде далее - циклы). Для проверки общей совместности системы, заданной матрицей s, достаточно проверить совместность некоторого подмножества подсистем, удовлетворяющего следующим критериям:
-
объединение ребер, входящих в циклы, соответствующие элементам подмножества, должно равняться множеству ребер графа ?'(w(s)) (критерий покрытия всех уравнений системы);
между любыми двумя циклами, соответствующими элементам подмножества, должен существовать путь, то есть цепь из других циклов, каждая соседняя пара циклов в которой имеет хотя бы одно общее ребро.
Возможность выбора подсистем множеством различных способов позволила разработать методику выбора подмножества подсистем, удовлетворяющего приведенным выше критериям и требующего минимального количества операций для проверки совместности. Припишем каждому циклу в графе ?'(w(s)) меру, пропорциональную вычислительной трудоемкости его проверки. Данный параметр можно принять прямо пропорциональным (например, равным) количеству ребер в цикле. Определим отображение ?: (G/?)/?' -> H, где H - множество гиперграфов, следующим образом. Сопоставим каждому ребру графа-прообраза вершину в графе-образе, а каждому циклу - ребро (возможно степени выше 2).
Таким образом, в новом пространстве каждому уравнению системы ограничений соответствует вершина, а каждой потенциально несовместной подсистеме - ребро гиперграфа. Рассмотрим, например, граф gX , изображенный на рис. 1, соответствующий системе с 5 переменными, 6 связанными уравнениями и 3 простыми циклами. Условная стоимость проверки циклов A, B и C соответственно равна 3, 4 и 5 единицам.
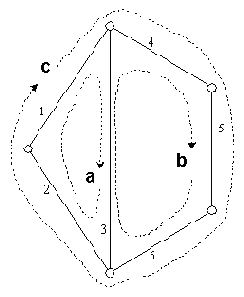
Рис. 1. Граф gX
Отображение ? переводит данный граф в гиперграф, изображенный на рис. 2.
