Оценка вычислительной трудоемкости предлагаемой методики
Для системы n уравнений с n неизвестными при отсутствии выборок из массива (хранящего информацию о перестановках строк и столбцов) общая вычислительная трудоемкость вывода инвариантов подобия равна количеству операций процессора
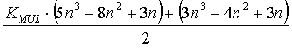 |
12 |
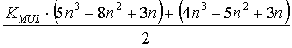 |
13 |
Здесь KMUL - коэффициент вычислительной трудоемкости операции целочисленного умножения по сравнению с операцией целочисленного сложения для данной аппаратной платформы. Например, для процессоров класса Intel Pentium значение этого коэффициента составляет 6-10 раз, для процессоров класса Intel 8086 может достигать 20-40 раз. При возможности реализации кэширования с высокой частотой попадания в кэш значение KMUL снижается до 2 раз.
Как следствие, выигрыш в вычислительной трудоемкости выделения инвариантов подобия в основном зависит от пропорций разбиения матрицы S на независимые компоненты. Так, например, при расслоении множества переменных на g подмножества равной мощности выигрыш K в вычислительной трудоемкости можно рассчитать по формуле:
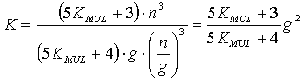 |
14 |
При этом выигрыш будет больше единицы при любом значении g
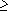
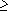
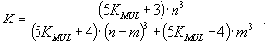 |
15 |
Разрешим неравенство
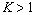 |
16 |
Эквивалентные преобразования (16) с учетом (15) приводят к условию
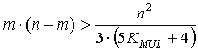 |
17 |
Учитывая, что нашей задачей является отыскание наименьшего m, превращающего неравенство (17) в истинное, будем считать, что
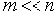 |
18 |
Тогда возможно принять
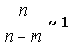 |
19 |
и неравенство (17) приобретает окончательный вид
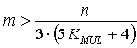 |
20 |
Как уже было указано, минимальное значение KMUL с применением технологии кэширования составляет 2 раза, без кэширования на современных аппаратных платформах - 6 раз. С учетом этого коэффициент в знаменателе неравенства (20) для кэш-реализаций составляет 42 и более, для реализаций без кэширования - 100 и более раз, что на практике приводит к выигрышу в вычислительной трудоемкости выделения инвариантов подобия уже при отделении хотя бы одной независимой переменной.
Таким образом, при наличии в графе w(S) нескольких связных компонент использование методики обнаружений аномалий на основе инвариантов подобия практически оправдано. При этом вычислительные затраты на поиск и выделение связных компонент в алгоритме вычислительных процессов по сравнению с вычислительной трудоемкостью вывода инвариантов подобия не значительны.
